As I briefly mentioned in a previous post, the bulk of my Ph.D. thesis consists of a conglomeration of three fairly disconnected publications. In order to lend some semblance of coherence to the thesis as a whole, I had no choice but to write a fairly general Introduction section starting with a quick historical overview of the genesis of cosmology as a field of scientific enquiry – so that it could more or less smoothly (although admittedly not seamlessly) branch out into three different directions. Without a doubt, the search for original references to populate this section was one of the most interesting and rewarding aspects of my thesis-writing process.
You see, when I set out to write the beginning of this section I had a very clear idea of what I wanted to write. About a dozen years earlier, I had been drawn to the world of theoretical physics by a few chance encounters with popular books on cosmology1, all of which included excellent (and much broader than I needed) introductions to the topic. A few years into my undergraduate degree, the basic structure of my mental model of the history of physics had been mostly fixed by a combination of such books and discussions with fellow students and a few teachers (who I assume were mostly sourcing their facts from similar books and discussions). Of course such books and discussions are not appropriate references for a Ph.D. thesis, but it seemed all I had to do was essentially summarise this mental image of mine and track down the original references to support it. Perhaps unsurprisingly, this search for original references led me to a few unexpected discoveries. To be clear, it did not upend my view of the history of science or anything close to that; but it did force me to review my understanding of how cosmology came about (and particularly of the role of some well-known individuals in it).
In the future, I expect to write about a number of physics topics here. As modern physics is a complex discipline which relies heavily on fairly advanced mathematics and non-intuitive concepts which have accumulated over the centuries, it helps to be able to point readers to sources where basics are discussed at an appropriately basic level (without, you know, telling them to go read whole books2). Therefore, I have cunningly decided to write a little series of posts3 ostensively going over these interesting surprises I encountered whilst writing my Introduction – all the while sneakily taking the opportunity to introduce some “basic” concepts my own way.
Albert Einstein and General Relativity
Albert Einstein is, without a doubt, the most famous physicist – nay, scientist – ever. His surname has become synonymous with “genius”, his face is universally recognisable (and a template for the “crazy scientist” stereotype, often with the addition of an out-of-character lab coat), and his quotes and misquotes are almost as ubiquitous as cats on the Internet.

The main reason a memeable scruffy physicist reached such a stellar status is his 1915 theory of General Relativity. At the time, it was publicised worldwide as supplanting Isaac Newton’s theory of universal gravitation, and therefore overthrowing the old Lucasian professor from his scientific throne. That it successfully does that is out of the question today (although it is likely to be incomplete itself), but what does this singular4 theory actually say?
It’s all about spacetime
General relativity isn’t called General Relativity just to emphasise how high-ranking it is; but rather to indicate that it is the more general version of Einstein’s elder brainchild: the theory of Special Relativity (the topic of a previous post). Special Relativity, in its simplest form, describes how lengths and times appear different to different observers moving at constant speed relative to each other (as a result of requiring the speed of light in vacuum to be the same for everyone5). A more insightful way of stating it, however, is in terms of quantities these observers can actually agree on. From this point of view, the geometric function known as the Minkowski metric plays a central role.
The Minkowski metric is a function that tells us the “distance”6 between two events, viewed as points in a four-dimensional space whose coordinates correspond to when and where they happened. If we refer coordinates in time by t and spatial coordinates by (x,y,z), and further denote the speed of light in vacuum by c, the distance between two events with spacetime coordinates (t1,x1,y1,z1) and (t2,x2,y2,z2) is given by
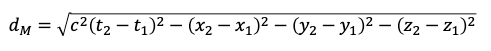
which in Special Relativity is the same for all observers moving at constant velocities relative to each other.
General Relativity is considerably more mathematically complex than Special Relativity (which is why it took Einstein a whole decade to get from the latter to the former, and why I shan’t endeavour to derive it in this post). Nevertheless, in a sense, its fundamental building block is the same: the spacetime metric, that allows us to define an objective four-dimensional distance and to calculate how time and space seem to change for different observers. The additional complexity comes from the fact that in the General case this metric is a function that can change in space and time depending on the distribution of matter and energy in the Universe. In particular, extreme distributions of matter and energy may dramatically change the shape of spacetime: as in the glamorous case of black holes (where there are literal holes in spacetime; i.e., regions where the metric is not defined) or in the more obscure case of cosmic strings (where you can have circles with less than 360 degrees).
Spacetime and gravity
The crowning achievement of General Relativity is its description of gravity as a result of the spacetime metric. According to Newton’s first law, bodies on which no force acts are expected to move in straight lines at constant speed. Conversely, when bodies move in more complex manners it’s because some force is acting on them. Newton’s greatest feat was the description of a gravitational force which is felt by all bodies with mass in the Universe, and which is sufficient to explain both the accelerated fall of apples on Earth and the elliptical orbits of planets around the Sun. In Einstein’s relativity, however, this fundamental force is actually nothing but Newton’s first law in a distorted spacetime: i.e., both apples on Earth and planets in the solar system move along straight lines at constant speed, but the concepts of speed and straight line are different from what they’d be in the absence of surrounding matter7.
Einstein’s field equations (an overview with no actual equations)
The intellectual monument that is General Relativity culminates in an elegant set of equations known as the Einstein field equations. Without going into details, what you need to know about these equations is that they relate quantities derived from the spacetime metric in a given region of spacetime to quantities defined by the local matter and energy distribution in that same region. In other words, if you know the matter and energy distribution in a given four-dimensional region (e.g., if you know the orbits and masses of the stars and planets in a given region of space), these equations will tell you the spacetime metric in that region (which you can, e.g., use to calculate the motion of small objects, like spaceships, travelling through that region). Conversely, if you happen to know the spacetime metric, these equations will give you the corresponding matter and energy distribution (i.e., just like with Newtonian gravity, you can learn about the positions of large bodies if you know enough about the orbits of smaller ones).
One key thing to keep in mind is that when a physicist says something is elegant it doesn’t necessarily mean it is easy to solve. Often it just means we can write it in such a way that its complexity is disguised by simple notation – and in a way that is the case with the Einstein field equations. A physicist writing them down will typically write the whole thing in one short line, possibly even giving the wrong impression that there is only a single equation to solve. In fact, the condensed notation typically used is hiding 16 equations (the square of the number of spacetime dimensions). Granted, some of these equations turn out to be equivalent to each other, and following some non-trivial mathematical gymnastics you can cut these down to 6 independent equations – but that is still a lot! As it happens, these equations are extraordinarily hard to solve: so much so that Einstein is said to have originally remarked he didn’t expect any exact solutions to be found! (The first one was published the year after.)
The cosmological constant (or lack thereof)
One way to derive the Einstein field equations is to start by making [deliberately not included here] intelligent arguments about which sorts of terms are mathematically allowed to feature in the desired equations. Then the relations between the “surviving” terms can be found using the mathematical consequences of physical constraints (e.g., requiring that for low densities and energies we end up with something equivalent to Newton’s gravity). Einstein did an excellent job of juggling all these different constraints; particularly given that in 1915 he did not know a key mathematical result which he ended up postulating entirely on physical grounds8.
Unfortunately, there are some mathematically relevant terms which cannot be decisively struck out using intelligent arguments and purely physical reasoning. These are usually dealt with by either further requiring the simplest possible set of equations that describes relativistic gravity, or neglecting terms that are irrelevant unless you’re in a very high-density environment (such a black hole)9. Most “superfluous” terms can be successfully dropped in this manner, but there is one notable exception: the term that has come to be known as the cosmological constant.
The cosmological constant is a special term, among other things, because it can be written on both sides of the Einstein field equations. That is, its addition to the equations can be equally motivated by it representing a “fundamental” aspect of gravity or by the presence of a particular energy distribution – a vacuum energy (and corresponding pressure) that is equally felt everywhere in the Universe10.
In his original formulation of General Relativity, Einstein is supposed to have left such a term out of the field equations simply due to his insistence on pursuing the simplest possible set of equations.
Einstein’s biggest blunder
No exploration of the work of Albert Einstein can be complete without a description of what has become universally known as “his biggest blunder”. This epithet is probably derived from Einstein’s own assessment of the blunder in question, as reported by George Gamow. The story behind it has been recounted countless times in books and lectures, often with subtle but (as I found out the hard way) meaningful variations. As it turns out, the blunder may not have been that big, or a blunder at all. At any rate, to my surprise, it seems that what he deemed to be a blunder was not exactly what people most often claim.
The typical story
In case you’ve never come across this story, here follows a typical plot of “Einstein’s Biggest Blunder”.
In 1915, Einstein upended the world of theoretical physics with his revolutionary theory of General Relativity. Even though he wouldn’t bask in the glory of its observational verification until 1919, the mathematical beauty of his theory had Einstein immediately convinced it was true and encouraged him to apply it to the Universe as a whole. The result came out in 1917 in yet another revolutionary paper which essentially marks the birth of modern cosmology. However, there was a big problem in this paper. As we now know, applying General Relativity to the Universe as a whole generically leads to a Universe which is either expanding or contracting. Einstein (typically motivated by a certain philosophical inflexibility) refused to accept such a dynamical Universe as true, and instead decided to modify his field equations to include the cosmological constant term; which he postulated to have just the right value to allow the Universe to be static. This a posteriori move to “fix” the Universe prevented Einstein from accepting the natural consequence of his own favourite version of the field equations. Had he not done so, Einstein would have predicted the expansion of the Universe more than a full decade before its observational discovery. This, it is said, is what Einstein himself declared to be his “biggest blunder”.
Usually there’s a bit of an epilogue to this story. Decades after Einstein abandoned the cosmological constant in favour of the simplest version of General Relativity which did conform to the then-apparent reality of an expanding Universe, astronomers realised the Universe’s expansion appeared to be accelerating (rather than decelerating as expected in this scenario). This anomalous acceleration, it turns out, can be perfectly explained by the presence of a small cosmological constant in Einstein’s field equations. In the end, Einstein’s rejection of the cosmological constant also prevented him from predicting the acceleration of the Universe’s expansion decades before its observational discovery. What a big blunder indeed! (OK, to be fair, nobody seriously thinks it reasonable that Einstein would have predicted an accelerated expansion at a time when data fit a simpler model perfectly. It does come across as a bit of posthumously rubbing salt in a wound though.)
The actual story
Thinking of including a (somewhat) more sober version of the above story in my thesis’ Introduction, I managed to chase down an English translation of Einstein’s 1917 foundational paper. What I read more than sobered my view of this famous episode.
First of all, I’d like to point out this is a truly delightful paper for a theoretical physicist to read11. Nowadays, applying General Relativity to the whole Universe is a feat easily accomplished by a Master’s student thanks to the ridiculous simplifying power of the FLRW metric (a simple class of metric functions that happen to be the only possible solutions for the metric of an homogeneous and isotropic Universe). Crucially, this powerful result was not known in 1917; and thus Einstein had to do a lot of mathematical heavy lifting to make up for it12. As a modern student reading this paper, I couldn’t help feel like I was seeing through the eyes of a very short-sighted Sherlock Holmes: constantly making far-reaching deductions out of small details from a big picture he was just unable to see (and which I had the unfair benefit of knowing in advance). Yet, throughout the paper, Einstein never loses sight of the physics to get lost in the mathematical complexities – he always manages to resurface from the equations with a physical insight to inform his next step. Again, it is a truly delightful paper for a theoretical physicist to read. Of course it’s not perfect (how could it be, at something the likes of which literally nobody had attempted before, lacking all but the most basic of tools?), but for a human achievement it’s still remarkable.
Einstein’s actual goal with this work was not so much to make predictions about the world as to test whether his theory could be taken seriously when “followed through to the finish or whether it leads to contradictions”. In other words, with his theory fresh out of the oven, his concern was to make sure it was consistent rather than to use it to contradict the astronomical consensus of the time. Einstein goes about this goal by subjecting his theory to a test in which Newton’s gravity does particularly poorly: by applying it to the whole Universe and seeing if he could get a coherent model out of it.
At this time, the known Universe consisted of little more than our own galaxy. It was thought to be approximately spherical with a radius of no more than 104 light-years, with little or nothing beyond that (compare that with the 93 billion light-years we can observe today). Importantly, this notion of the Universe was hard to reconcile with Newton’s gravitational mechanics13. Using Einstein’s General Relativity, it seemed the task was similarly hard.
After a “rough and winding road”, Einstein finds he can produce a cosmological model out of his theory if:
(1) he assumes the Universe is spatially closed (i.e., that space is like a 3D version of the surface of a sphere; so that travelling indefinitely in the same direction will eventually take you around it);
(2) he allows a cosmological constant term in his field equations.
Einstein doesn’t ever see that the Universe is allowed to expand or contract without the cosmological constant. Although he probably wouldn’t have accepted that result had he seen it (as he didn’t when others proposed the same14), that wasn’t even an option here as the requirement that the Universe be (approximately) static was a condition in his equations from the start (in keeping with what was known at the time).
Einstein put his theory through a rigorous test of consistency: and in the end the theory was forced to slightly adjust in order to produce a consistent model of the world. This was not a blunder, but good scientific practice: to do the opposite would have been intellectually arrogant beyond any reasonable justification.
Why then did Einstein reportedly refer to this as his biggest blunder? Presumably, it’s because of theoretical considerations he failed to take into account: namely that the model he had produced was actually unstable in the sense that it couldn’t stand small fluctuations in density (which must always exist in practice); which would have caused that Universe to either expand or contract indefnitely.
The actual blunder
Even Einstein’s failure to notice his model’s instability, I would argue, can hardly be considered a blunder in the face of the amount of work required to do what was done in this paper. I find it hard to fault him for that sort of thing – which is standard to consider now, but certainly wasn’t back then (remember this was all uncharted territory; he was literally inventing a new field!).
A big blunder did come of this, but not in this 1917 paper. The actual big blunder, I would argue, came years later when, faced with actual mathematical solutions for a non-static Universe (relying on the sorts of useful tools he lacked in 1917), Einstein failed to acknowledge their importance and to re-evaluate his own model. His stubborn denial then, I would argue, did set our understanding of cosmology back by almost a decade.
In conclusion, Einstein’s assessment of his “biggest blunder” strikes me as both too harsh on that particular work and too lenient on his subsequent mistakes. It is tempting to always depict Einstein as the “last genius in his ivory tower”, and the biggest blunder myth feeds this view by burdening this one dead genius with the responsibility to carry a whole field on his giant shoulders. Instead, we should appreciate his undeniably brilliant contributions, whilst also critically evaluating the way in which his interactions with the wider community did at times prevent good physics from flourishing in due time – but that is a story for another time.
Footnotes
1. Most notably, in no particular order: Stephen Hawking’s Brief History of Time; João Magueijo’s Faster Than The Speed Of Light; and Dead Famous’ Albert Einstein and His Inflatable Universe (a fun biographical work with lots of good science by Mike Goldsmith).
2. Which, incidentally, is a much better way of learning the basics if you can spare the time. See footnote above for good examples.
3. At the moment I’m envisioning three parts in this series, although I wouldn’t rule out a fourth just yet.
4. Pun very much intended.
5. Seriously, just read my previous post about it. It’s all there.
6. Mathematically, we say a function is a metric (or distance) if it tells us the distance between two points: is never negative (which is true of the Minkowski metric for points inside the same light cone); is symmetric (i.e., the distance between A and B is the same as the distance between B and A); and verifies the triangle inequality (the property that the length of one side of a triangle can never be greater than the sum of the other two’s). In addition to this, the metrics discussed in this post possess the additional property that they can naturally be extended to define a concept of angle. As long as these properties are observed, these metrics can be used to do geometry in a familiar (albeit abstract) way.
7. Speed changes similarly to how it does in Special Relativity, and a straight line is defined as the shortest route between its two end points (according to the spacetime metric).
8. If I’m not mistaken, the result in question is one of the Bianchi identities. This issue is supposedly mentioned in Abraham Pais’ book Subtle is the Lord. I must confess I’ve only heard of this from a professor’s mouth.
9. Modern attempts to extend Einstein’s theory typically rely on invoking some of these terms which can be relevant in extreme scenarios.
10. To make matters more complicated, we now know such a vacuum energy must exist due to quantum mechanical effects. However, this energy does not seem in agreement with cosmological observations by itself. One modern way to ignore this problem is to just assume this effect is almost exactly cancelled by a “true” cosmological constant on the curvature side of Einstein’s equations.
11. I do not recommend its reading to people not familiar with the mathematical details of the theory. Side effects may include paranoia and seeing metric tensors everywhere.
12. Really, I can’t properly emphasise how central this result is for cosmology as we know it. Certainly no part of my thesis beyond the Introduction would be possible without it. To do cosmology without this result, as Einstein did, is something akin to plowing a field with one’s bare hands.
13. In this paper, Einstein speaks of the necessity that the Newtonian Universe should have a finite “bulk” of this sort so that too many far away celestial objects don’t end up spoiling the predictions of Newton’s gravity taking into account what is close to us. However, random collisions between celestial bodies should fairly often result in too many bodies acquiring enough velocity to escape the gravitational pull of this bulk and spoiling these predictions anyway.
14. Stay tuned. These others will be discussed in upcoming posts in this series.
3 thoughts on “Things I learnt writing my thesis’ Introduction (Part 1): Einstein’s not so big blunder”